Movimientos y Aceleraciones: noviembre 2016

Aceleracion media

Se define la aceleración media entre dos puntos P1 y P2 como la división de la variación de la velocidad y el tiempo transcurrido entre ambos puntos:

a→m=v→2−v→1t2−t1=Δv→Δt

→m : Es la aceleración media del punto material
v→1 ,v→2 : Vectores velocidad en los puntos P1 y P2respectivamente
t1,t2: Instantes de tiempo inicial y final respectivamente
Δv→ : Variación de la velocidad entre los puntos inicial y final P1 y P2
Δt : Tiempo invertido en realizar el movimiento entre P1 y P2

Caracteristicas:

La ecuación de dimensiones de la aceleración media es [am] = LT-2
Unidad de medida en el Sistema Internacional (S.I.) de la aceleración es el metro por segundo al cuadrado (m/s2). Un cuerpo con una aceleración de 1 m/s2 varía su velocidad en 1 metro/segundo cada segundo.
Su módulo (el "tamaño" del vector) es igual al módulo del vector variación de la velocidad dividido entre el tiempo transcurrido
Su dirección y su sentido son las mismas que las del vector variación de la velocidad

Ejercicios resueltos:

Un camión de bomberos aumenta su velocidad de 0 a 21 m/s hacia el Este, en 3.5 segundos. ¿Cuál es su aceleración?

Dado:

Velocidad inicial (Vi): 0 m/s
Velocidad final (Vf): 21 m/s, Este
Tiempo (t): 3.5 segundos
Desconocida: Aceleración a=?

Ecuación básica:

Solución:

Respuesta: Para indicar la aceleración debes indicar también la dirección. Como el objeto se mueve hacia el este la respuesta es: 6m/s² , Este

El resultado indica que por cada segundo que transcurre, la velocidad del auto aumenta por 6.0 m/s

. Calcula el tiempo necesario para que un automóvil que se mueve con una rapidez de 100 km/h recorra una distancia de 200 km.

Para resolver este problema es necesario despejar la ecuación de rapidez para obtener la fórmula que nos permitirá calcular el tiempo transcurrido:

Ejercicios a resolver:

1. Un avión vuela en línea recta hacia el norte durante 15 min si lleva una velocidad de 700 km/h, ¿cuál es la distancia que recorre durante ese tiempo? Nota: se deben transformar los minutos a horas para poder tener unidades iguales en todos los datos. R= 175 km

2. Una pelota recorre 20 m hacia la derecha y luego 10 m hacia la izquierda, todo en un lapso de tiempo de 10 s, ¿cuál es su velocidad y rapidez? R= r= 3 m/s porque se considera la distancia total de todo el recorrido, es decir 30 m; v= 1 m/s hacia la derecha porque el vector del desplazamiento se dibuja desde el punto inicial hasta el punto final del recorrido, entonces la longitud es de 10 m hacia la derecha.

Videos:

Conclusión:

 Si queremos que la aceleración y velocidad de un móvil este en función del tiempo solamente, debemos derivarlo.

 Un cuerpo puede tener aceleración a pesar de no tener velocidad.

Links:

https://www.fisicalab.com/apartado/aceleracion-media

https://sites.google.com/site/timesolar/cinematica/ejemplosaceleracion

Aceleracion instantanea:

La aceleración instantánea de un cuerpo es la que tiene el cuerpo en un instante específico, en un punto determinado de su trayectoria. Para definir el concepto de aceleración instantánea con precisión podemos partir de la aceleración media en un intervalo y hacer este infinitamente pequeño (Δt→0 ). Este proceso es análogo al que seguíamos con la velocidad media para calcular la velocidad instantánea.

Se define la aceleración instantánea, o simplemente aceleración, como el límite de la aceleración media cuando el intervalo de tiempo considerado tiende a 0. También se define de manera equivalente como la derivada de la velocidad respecto al tiempo. Su expresión viene dada por:

a \to = lim Δ t \to 0 a \to m = lim Δ t \to 0 Δ v \to Δ t = d v \to d t

donde:

a→ : Es la aceleración del cuerpo
a→m : Vector aceleración media
Δv→ : Vector variación de la velocidad
Δ t : Intervalo de tiempo que tiende a 0, es decir, un intervalo infinitamente pequeño

La aceleración es una magnitud vectorial. La ecuación de dimensiones de la aceleración instantánea es [a] = LT-2 y por tanto su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado [m/s2].

Caracteristicas:

La aceleración es una magnitud vectorial. La ecuación de dimensiones de la aceleración instantánea es [a] = LT-2 y por tanto su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado [m/s2].

Podrás encontrar el vector aceleración escrito mediante sus componentes cartesianas quedando:

vector aceleración en 3 dimensiones coordenadas cartesianas:

$a \to = a x i \to + a y j \to + a z j \to = (lim Δ t \to 0 Δ v x Δ t) i \to + (lim Δ t \to 0 Δ v y Δ t) j \to + (lim Δ t \to 0 Δ v z Δ t) j \to = d v x d t i \to + d v y d t j \to + d v x d t j \to$
vector aceleración en 2 dimensiones coordenadas cartesianas:

$a \to = a x i \to + a y j \to = (lim Δ t \to 0 Δ v x Δ t) i \to + (lim Δ t \to 0 Δ v y Δ t) j \to = d v x d t i \to + d v y d t j \to$

Como puedes observar, la aceleración instantánea es una magnitud vectorial que cumple:

Su módulo se puede expresar:
- Mediante coordenadas cartesianas en 3 dimensiones:
  
  $∣ ∣ a \to ∣ ∣ = a 2 x + a 2 y + a 2 z - - - - - - - - - - \sqrt$
- Mediante coordenadas cartesianas en 2 dimensiones:
  
  $∣ ∣ a \to ∣ ∣ = a 2 x + a 2 y - - - - - - \sqrt$
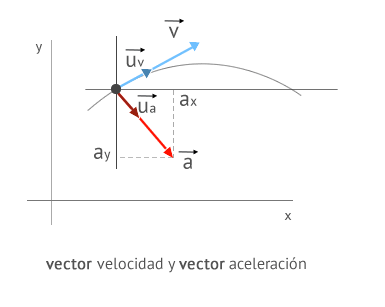
Su dirección y sentido, en general, no coincide con la del vector velocidad sino que dependen del cambio que experimente esta.

Ejercicios resueltos:

Un meteorito se desplaza por el cielo con una velocidad v⃗(t) = (1+4·t) i⃗+t2j⃗ m. Calcular:

a) Su aceleración media entre los instantes t1=2 sg y t2=4 sg.
b) Su aceleración en el instante t3=6 sg.

Solución

Cuestión a)

Datos

v⃗(t) = (1+4·t) i⃗+t2 j⃗ m

t1=2 sg y t2=4 sg

Resolución

Para calcular la aceleración media debemos hacer uso de la siguiente ecuación:

a \to m = v \to 2 - v \to 1 t 2 - t 1 = Δ v \to Δ t

Conocemos t1 y t2. Ahora nos falta calcular la velocidad en el instante t1 (v⃗1) y en el instante t2 (v⃗2). Para ello basta sustituir en la ecuación de velocidad que nos han proporcionado en el enunciado del ejercicio:

Para t1=2 sg

v \to 1 = v (2) = (1 + 4 \cdot 2) \cdot i \to + (2) 2 \cdot j \to m / s g \Rightarrow v \to 1 = 9 \cdot i \to + 4 \cdot j \to m / s g

Para t2=4 sg

v \to 2 = v \to (4) = (1 + 4 \cdot 4) \cdot i \to + (4) 2 \cdot j \to m / s g \Rightarrow v \to 2 = 17 \cdot i \to + 16 \cdot j \to m / s g

Sustituyendo en la primera ecuación:

a \to m = ( 17 - 9 ) \cdot i \to + ( 16 - 4 ) \cdot j \to 4 - 2 m / s g 2 \Rightarrow a \to m = 8 \cdot i \to + 12 \cdot j \to 2 m / s g 2 \Rightarrow a \to m = 4 \cdot i \to + 6 \cdot j \to m / s g

Cuestión b)

Datos

v⃗(t) = (1+4·t) i⃗+t2 j⃗ m
t3= 6 sg

Resolución

Para calcular la aceleración en el instante t3 debemos calcular previamente la aceleración instantánea:

a \to = lim Δ t \to 0 a \to m = lim Δ t \to 0 Δ v \to Δ t = d v \to d t

Aplicando la derivada de la velocidad con respecto al tiempo obtenemos que:

a (t) - \to - = 4 \cdot i \to + 2 \cdot t \cdot j \to m / s g 2

y sustituyendo el valor de t3=6 sg.

videos:

Conclusión:

 Al determinar la relación entre la velocidad promedio y la velocidad instantánea nos damos cuenta que la velocidad instantánea puede ser calculada obteniendo experimentalmente la velocidad promedio.

 Tenemos que tomar en cuenta los factores que influyen en el movimiento a analizar para que nuestros cálculos sean más precisos.

 Debemos considerar que existen conceptos que en cinemática se relacionan pero que no son semejantes como rapidez y velocidad o velocidad media y velocidad instantánea.

 Al hallar la aceleración, velocidad o posición de un objeto o partícula debemos tener un sistema de referencia ya que de acuerdo a este dicho objeto o partícula podría realizar un movimiento parabólico, de caída libre, circunferencial

Links:

https://www.fisicalab.com/apartado/aceleracion-instantanea

https://sites.google.com/site/timesolar/cinematica/ejemplosaceleracion

MRU(movimiento rectilineo uniforme)

Un movimiento es rectilíneo cuando un objeto describe una trayectoria recta respecto a un observador, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula.

Nótese que el movimiento rectilíneo puede ser también no uniforme, y en ese caso la relación entre la posición y el tiempo es algo más compleja.

Caracteristicas:

Movimiento que se realiza sobre una línea recta.
Velocidad constante; implica magnitud y dirección constantes.
La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
no hay aceleración

formulas:
dx=v.t

v=dx/t

t=dx/v

ejercicios resueltos:

Un avión se mueve en línea recta a una velocidad constante de 400 km/h durante 1,5 h de su recorrido. ¿Qué distancia recorrió en ese tiempo?

Datos

v = 400 k/h

t = 1,5 h

d = ?

Solución

Despeje

Sustituyendo

El avión había recorrido al cabo de ese tiempo una distancia de 600 km.

Problema resuelto 2

Analiza la tabla de datos del movimiento de un corredor en un tramo recto de una competencia. Determina:

Tabla del corredor
distancia (m)	0	10	20	30	40	50
tiempo (s)	0	2	4	6	8	10

a) valor de la velocidad ha corrido 10 m, 30 m, y 50 m.

b) tipo de movimiento del corredor atendiendo al valor de su velocidad y al valor de su velocidad. Argumenta.

c) distancia recorrido a los 4 s de iniciado el movimiento.

Solución

a) En todos los casos se debe calcular la velocidad del corredor mediante la ecuación:

Sustitución de la fórmula (en la ecuación sustituir la letra por el valor de los datos)

b) El tipo de movimiento es rectilíneo uniforme porque la velocidad permanece constante durante toda la carrera.

c) A los 4 s el corredor recorrió 20 m.

Ejercicios para resolver:

1)¿Qué tiempo demorará una señal de radio enviada desde la Tierra en llegar a la Luna?

Dato útil

Distancia desde la Tierra hasta la Luna (300 000 km/s )

2)En cierto lugar de la Ciudad de la Habana se escucha el “Cañonazo” a las 9 h y 20 s ¿A qué distancia de la “Fortaleza de la Cabaña” se encontrará dicho lugar?

3)La figura es la representación gráfica de la velocidad con respecto al tiempo del movimiento en línea recta de un corredor.

a) ¿Qué tipo de movimiento lleva el corredor? Explica.

b) Determina la distancia recorrida por él en 6 s. Represéntala en la gráfica.

Videos:

Conclusión:

En conclusión podemos decir que el movimiento rectilíneo uniforme se produce cuando la velocidad es constante. Se dice que es "uniforme" cuando no hay cambios en la velocidad, es decir se mueve de una misma forma, velocidad igual o "constante”. La velocidad es igual a la distancia entre el tiempo. Este tipo de movimiento no presenta variación en su velocidad a menos que una fuerza extra actué sobre el objeto pero ahí ya se llamaría movimiento rectilíneo uniformemente variado. Su magnitud y velocidad no cambia.

links:

https://es.wikipedia.org/wiki/Movimiento_rectil%C3%ADneo_uniforme

http://fisica.cubaeduca.cu/medias/interactividades/mru/co/modulo_contenido_5.html

Movimiento parabólico

Se denomina movimiento parabólico, al movimiento realizado por cualquier objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical acelerado.

La composición de un movimiento uniforme y otro uniformemente acelerado resulta un movimiento cuya trayectoria es una parábola.

Un MRU horizontal de velocidad vx constante.

Un MRUA vertical con velocidad inicial voy hacia arriba.

Denominamos proyectil a todo cuerpo que una vez lanzado se mueve solo bajo la aceleración de la gravedad.

Características:

· Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.

· Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales)

· La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.

· Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.

· Se puede analizar el movimiento en vertical independientemente del horizontal.

Ejercicios resueltos:

Calcular la distancia, la altura y el tiempo de caída de un tiro parabólico que lleva una velocidad de 30m/s y forma una ángulo de 60° con la horizontal.

Primero calculamos la distancia recorrida.

d= v12sen2a / g = (30m/s)2 sen 2(60°) / 9.8 m/s2 = 158.99 m

Ahora la altura alcanzada.

h= v21sen2a / 2g= (30 m/s)2 sen2 (60°) / 2(9.8 m/s2) = 36.29 m

Por último el tiempo realizado.

t= v1 sen a / g= 30 m/s (sen 60°) / 9.8 m/s2 = 2.85 s

Ejercicios para resolver:

Se patea un balón de futbol a una velocidad de 30 km/h formando un ángulo de 37grados:

a) indicar su tiempo de vuelo

b) distancia recorrida del balón.

Se lanza una ballesta con una velocidad de 40 km/h formando una angulo de 45 grados. Indicar:

A) Su tiempo de vuelo

b) distancia que recorre la ballesta.

videos:

Movimientos y Aceleraciones

jueves, 24 de noviembre de 2016

movimientos y Aceleraciones.

Solución

Problema resuelto 2